Some Unusual Features of Mazar and Zhong (2010)
And the Bad Old Days of Psychological Science
Big thanks to Old Man Gloom for assists, analysis suggestions, and sanity checking. Please consider this co-authored by him, even if I can’t figure out the Substack multiple authors thing.
I have a complicated relationship with the journal Psychological Science.
On one hand, I think they’ve made great strides in addressing methodological problems in experimental psychology. They’ve had some reform-minded editorial staff who are largely responsible for shouldering the burden on this, and that’s how anything in difficult science gets done - gritted teeth. And they’ve just brought in a new editor who is one of the very few people that makes me think that social science isn’t just setting money on fire to produce witchcraft with regression.
On the other, I think a huge chunk of what they published circa ten years ago and before is like a suppurating wound in the side of scientific reform, a diabetic lesion that will never quite heal.
You can’t amputate, and unpublish decades worth of unreliable fairy stories for a variety of reasons, most of them practical. The size of the investigation would dwarf any of those that publishers claim they do, and would be considered an outrageous imposition.
But you can’t treat and manage the wound either - that would mean expecting everyone citing work from the Bad Old Days to have a full appreciation of just how strained and nonsensical a lot of it was. We can’t even get people to stop citing retractions, so this is a non-starter.
This problem, of course, is not limited to one journal, nor is PS afflicted with a particularly terminal case of the sillies. Other journals are likely worse, and have never gotten better, or have actively gotten worse. And: never forget that the consequences are low - at a high level, we waste little money and kill few people with the polite fictions of social science.
(This is why I have spent years thinking about shitty medical and policy research instead, even while I wasn’t publishing very much. The Plague certainly brought this problem into sharp relief for me. Bad medical research kills people. Bad policy derived from that research adds a layer of abstraction, then kills people.)
I haven’t been involved in the recent Gino and Ariely fuss over the last two years at all. I read about it in the newspaper, same as you. When it started, it was an interesting academic dust-up, and then over time became something else entirely.
But, perhaps weirdly, I also perceive a potential sense of karmic unfairness to it.
Not regular unfairness, shut up. It’s more that I find it vanishingly unlikely that there are two researchers who deserve to be in the line of fire while everyone else is a paragon of virtue.
This often happens under the ‘rotten apple’ model of bad scientists. It justifies exactly this situation, where some people put up against the wall, and everyone else gets to pearl-clutch. Because isn’t it terrible. Isn’t it just untoward. We would never do something like this, would we?
Something Diederik Stapel said has stuck with me for years:
I knew that this was at the outer limits of what was acceptable, or even beyond those limits in some cases, but… I wanted the results so badly. Plus, it worked in an earlier study, and the results were really almost, almost right, and it must be true because it’s so logical, and it was such a great idea, and I surely wasn’t the only person doing this sort of thing. What I did wasn’t whiter than white, but it wasn’t completely black either. It was gray, and it was what everyone did. How else did all those other researchers get all those great results?
How indeed.
This kind of thing makes me curious.
Footling Around In The Stormwater Drain Of Empiricism
With the above in mind, and with more time than sense, I found this paper in an idle moment. I was footling through citation chains, jumping from co-author to co-author, none of whom I recognise - I have not paid a single second’s attention to the field for a very long time.
If anything, it is all less consequential than I remember.
But, also, it seems… fun, building these castles in the sky. Maybe this is a consequence of me having the shit kicked out of me at startups for the last few years. If you put aside the monstrous arrogance of trying to derive broad principles of human behaviour from 59 white undergraduates at the University of Popped Collar, you do see a playfulness and creativity at work. It must be extremely satisfying if you actually derive anything useful from it.
In this rather unfocused curiosity, I found “Do Green Products Make Us Better People?” by Mazar and Zhong (2010). At time of writing, 1262 citations.
That is so many citations.
Happily, a combination of scite.ai (my not-so-secret weapon for traversing citation chains much faster than any other method) and Google Scholar (flawed as it may be) make it very straightforward to dart between papers at the speed of thought. Much to my curiosity, priming research still seems to be out there, battered somewhat, but still persisting.
Guess they missed the last ten years.
But none of this really matters. The crisis has been great for psychology. In terms of methodological progress, this has been the best decade in my lifetime. Standards have been tightened up, research is better, samples are larger. People pre-register their experimental plans and their plans for analysis. And behavioral priming research is effectively dead. Although the researchers never conceded, everyone now knows that it's not a wise move for a graduate student to bet their job prospects on a priming study. The fact that social psychologists didn't change their minds is immaterial.
Kahneman, 2022.
Anyway, what’s this paper all about?
Consumer choices reflect not only price and quality preferences but also social and moral values, as witnessed in the remarkable growth of the global market for organic and environmentally friendly products. Building on recent research on behavioral priming and moral regulation, we found that mere exposure to green products and the purchase of such products lead to markedly different behavioral consequences. In line with the halo associated with green consumerism, results showed that people act more altruistically after mere exposure to green products than after mere exposure to conventional products. However, people act less altruistically and are more likely to cheat and steal after purchasing green products than after purchasing conventional products. Together, our studies show that consumption is connected to social and ethical behaviors more broadly across domains than previously thought.
So, this is a kind of … ego depletion for altruism.
Let’s look at the studies. There are three.
ONE
Fifty-nine students (32 female, 27 male) from the University of Toronto volunteered for a 5-min survey. They were randomly assigned to rate either a person who purchases organic foods and environmentally friendly products or a person who purchases conventional foods and products. They used a 7-point scale (1 = not at all, 7 = very) to indicate how cooperative, altruistic, and ethical they thought such a person is…. a person who purchases green products was rated as more cooperative (M = 4.75, SD = 1.37, vs. M = 3.62, SD = 1.76), t(57) = 2.76, p = .008, prep = .956; more altruistic (M = 5.07, SD = 1.01, vs. M = 3.36, SD = 1.23), t(57) = 5.81, p < .001, prep > .986; and more ethical (M = 5.55, SD = 1.44, vs. M = 3.36, SD = 1.70), t(57) = 5.35, p < .001, prep > .986.
(Ignore the ‘prep’ - it was an alternative method of reporting test statistics, that had two minor problems of (a) being a straightforward transform of the p-value and (b) not really working.)
So, we start with getting an idea of what these numbers might look like, and of course the journal has made this unnecessarily hard, because there’s no cell sizes. Not to worry, we can often infer those using GRIM. We need a denominator which can handle eventual means of 4.75, 5.07, 5.55 for one group, 3.62, 3.36 for the other. Then, we need them both to add to n=59.
The arseache here is: there isn’t a solution.
Let’s start with the control group, with a sample size of n1. n1 will produce a GRIM solution where the means of 3.62 and 3.36 can be produced. There are several less than the sample size (59):
n1=39 42 45 47 50 53 55 58
(Obviously, some of those are a bit bonkers if they’re a subset of n=59 participants - but they’re still possible.)
Next: the ‘green’ group (with a sample size of n2) will produce a GRIM solution where the means of 4.75, 5.07, and 5.55 can be produced. Again, some solutions:
n2=44 55 56
And also, again, the problem here is obviously that these are pretty bonkers cell sizes for n=59 total, and that no combination of the two groups above add to n=59.
(Combining GRIM tests like this, which I’ve referred to elsewhere but never fully explained, is very simple but also very powerful for retrieving lost sample sizes - if a solution exists, it comes screaming right out. If you have a lot of outputs, say, four means which are all derived from the same sample size, you can usually retrieve multiple cell sizes from a total n. It’s handy.)
Computationally, not much needs to happen. But I do have one cute element of this that I make for my own sanity during the process, which for want of a better term I call a ‘GRIM quilt’. The numbers below are all the possible means for every single cell size. Each row is a new unit (a row of 1ths, a row of 1/2s, a row of 1/3s, etc.) and each column is a cell size (n=1, 2, 3, up to 59 in this case).
The colored rays need to have vertical elements in the same column for the sample to potentially exist, because they associate potential sample sizes. In other words, red and blue in the same column, and green(s) and yellow in the same column.)
Anyway: it’s all rather confusing really, because it seems the cell sizes can’t exist as described without more information.
But - there is more information available!
Thanks to the diligent work of Old Man Gloom, and back in the day this really was a seminal observation on his part, we can RIVETS-hack this result a bit. Recall that any statistical test actually has a variable test statistic output determined by hidden figures. Let’s take that first result:
(M = 4.75, SD = 1.37, vs. M = 3.62, SD = 1.76), t(57) = 2.76, p = .008
A wrinkle most people miss is that test statistics are quite sensitive, even to numbers we can’t see at a 2dp level. Let’s assume for right now that the groups are almost equal, n=59 into n=29 and n=30.
In actual fact, the maximum case for t is the highest possible difference with the lowest possible SD, which is
(M = 4.7549…, SD = 1.365, vs. M = 3.615, SD = 1.755)
Th lowest case is the lowest difference with the highest possible SD
(M = 4.745, SD = 1.3749…, vs. M = 3.6249…, SD = 1.7649…)
Both of these have identical 2dp means and SDs, so they are the ‘same’. But the t-test output ranges between 2.778 and 2.713. While that’s not a tremendous range, it does allow for a curious amount of slop with regards to exact values. Here’s the fun bit: because a test like this just smashes the two cell sizes together in the denominator, we can use the maximum case above to find the cell size solutions that fit the t-values! Remember, we’re looking for t=2.76.
SO
n=29 vs n=30: t=2.778, at max value, see above. This works.
n=28 vs n=31: t=2.763, at max value. This works too.
n=27 vs n=32: t=2.745. This doesn’t. t is too low.
n=26 vs n=33: t=2.724. This even more doesn’t.
and so on down…
Basically, there are two working cell size solutions according to the t-test, and neither of them are compatible with GRIM.
It’s all good fun, but remember: it only works if the original data is in whole numbers. One single smartarse undergraduate putting a 4.20, or a 6.9, or answering on slider bar, or permitting half units, make the whole thing invalid. When you introduce proper granularity into the measurements, the whole thing goes to the dogs. Maybe there’s unreported exclusions, too.
Even so: bad sign. The paper doesn’t mention anything except a seven point scale.
Weird.
TWO
One hundred fifty-six students (95 female, 61 male) from the University of Toronto volunteered for an hour-long experiment in exchange for class credit. Participants were randomly assigned to one condition of a 2 (store: conventional vs. green) × 2 (action: mere exposure vs. purchase) between-participants design…
an initiator has money ($6) to allocate between him- or herself and a recipient. The initiator keeps whatever money he or she does not offer; the recipient can choose to accept or reject the offer, but this choice affects only the recipient’s own payoff…
Neither store type (conventional vs. green) nor action (mere exposure vs. purchase) had a significant main effect on the amount of money offered, F(1, 152) = 0.06, p = .806, prep = .271, and F(1, 152) = 0.27, p = .603, prep = .427, respectively. However, there was a significant interaction, F(1, 152) = 4.45, p = .037, prep = .897. Participants who were merely exposed to the green store shared more money (M = $2.12, SD = $1.40) than those who were merely exposed to the conventional store (M = $1.59, SD = $1.29), F(1, 152) = 2.85, p = .094, prep = .824. This pattern reversed in the purchasing conditions: Participants who had purchased in the green store shared less money (M = $1.76, SD = $1.40) than those who had purchased in the conventional store (M = $2.18, SD = $1.54), F(1, 152) = 1.69, p = .195, prep = .728.
So, this task seems goofy (this ‘modified dictator game’ seems to be modified to the point where the second party has no influence whatsoever, making it a game that should rightly be called ‘give people stuff or don’t, it doesn’t matter’) but I can easily recreate the 2*2 between ANOVA, seems like it’s calculated correctly. Trying to hack cell sizes out of this might be possible, but I can’t be bothered with the arseache.
THREE
Ninety undergraduate students (56 female, 34 male) from the University of Toronto volunteered for this experiment in exchange for $5 Canadian. Participants were randomly assigned to one of two stores (conventional vs. green). Upon arrival, each participant was seated at a desk equipped with a computer and one envelope containing $5 in various denominations.
In the first task, they were randomly assigned to make purchases in either the conventional or the green-product store, as in Experiment 2. Afterward, they engaged in an ostensibly unrelated visual perception task in which a box divided by a diagonal line was displayed on the computer screen (Mazar & Ariely, 2009). Participants were told that on each trial they would see a pattern of 20 dots scattered inside the box. The pattern would stay on the screen for 1 s, and the task was to press a key to indicate whether there were more dots on the left or right side of the diagonal line. Participants were paid 0.5¢ for each trial on which they indicated there were more dots on the left and 5¢ for each trial on which they indicated there were more dots on the right. The dots were always arranged such that one side clearly had more dots than the other side (15 vs. 5, 14 vs. 6, 13 vs. 7); thus, it was fairly easy to identify the correct answer. We emphasized that it was important to be as accurate as possible because the results would be used in designing future experiments.
The round with real pay consisted of 90 trials. On 40% of the trials, there were more dots on the right than on the left side (36 trials). Consequently, if participants were 100% accurate, they could make $2.07 in a task that lasted about 5 min. At the end of the 90th trial, participants saw a summary screen that showed the total amount of money they had earned and instructed them to pay themselves by taking out the corresponding amount from the provided envelope. Thus, in addition to having the opportunity to lie, participants could steal to increase their payoff.
We found a significant difference between conditions in performance on the dots task, t(79) = 2.26, p = .027, prep = .913. Participants who had purchased in the conventional store identified 42.5% (SD = 2.9%) of trials as having more dots on the right side; this percentage was not significantly different from the actual percentage (i.e., 40%), t(37) = 1.66, p = .106, prep = .811. Participants who had purchased in the green store, however, identified 51.4% (SD = 2.67%) of trials as having more dots on the right side—which suggests that they were lying to earn more money. Participants in the green-store condition earned on average $0.36 more than those in the conventional store condition. As noted, independently of deciding to lie, participants could steal by taking more money from the envelope than shown on the summary screen. Results for this measure were consistent with those for task performance: Participants in the green-store condition stole $0.48 more from the envelope than those in the conventional-store condition (M = $0.56, SD = $0.13, vs. M = $0.08, SD = $0.14), t(79) = 2.55, p = .013, prep = .942. Altogether, participants in the green-store condition left the experiment with on average $0.83 (SD = $0.23) more in their pockets than did participants in the conventional-store condition, t(70) = 3.55, p < .001, prep > .986.
(Nine participants failed to pay themselves. They were excluded from analyses.)
So, that’s only moderately convoluted. A few things here:
I pity the poor students going through this rigmarole to win half a cent per item
this isn’t ‘fairly easy’, I’d go more with ‘really quite trivial’. It seems reasonable to expect a floor value close to 36 ‘right’ answers that confer 5 cents (with 54 conferring 0.5 cents) - that’s where the $2.07 figure comes from.
as there appear to be no consequences whatsoever for lying in this task, someone pressing ‘right’ for every response would be 40% correct, but be conferred the princely sum of $4.50.
we finally have some goddamn cell sizes
Let’s start with what, to me, was the glaring oversight that led me to look through the whole paper thoroughly.
Participants who had purchased in the conventional store identified 42.5% (SD = 2.9%) … Participants who had purchased in the green store, however, identified 51.4% (SD = 2.67%)
This is, in a word, enormous. Let’s quantify it.
n=90 students, throw away n=9 who hate money as noted in the paper, and you have n=81.
Now, the control is being compared to the expected outcome, 40%, so t(37) from the one-sample t-test means n=38, which means intervention n=43.
Cell sizes. What a luxury.
So, we have 42.5% (2.9%) n=38 vs. 51.4% (2.67%) n=43, which is t=14.3785, which is a Cohen’s d of 3.2.
This is, obviously, beyond wrong and into ‘slightly mad’.
It is also, given the topic of the paper, the most extraordinary success. It demonstrates overwhelmingly that this whole ‘green product exposure’ priming is working incredibly well.
So, it’s very strange indeed that the calculation included in the above was never mentioned in the paper.
The obvious explanation when any effect is absolutely gigantic, and the very first thing we look for when going through it, is whether or not someone has confused SD (standard deviation) with SEM (standard error of the mean). This was the first aberrant detail I noticed while reading through the paper that made me look a bit closer.
This is an minor irritation for expurgating the paper, but also extremely common. Here’s some context on just how unremarkable this is from 20 years ago.
In this situation, we always test the SE-to-SD conversion, so:
42.5% (2.9%*38^0.5) n=38 vs. 51.4% (2.67%*43^0.5) n=43, i.e.
42.5% (17.88) n=38 vs. 51.4% (17.51) n=43
That looks a lot more realistic, and returns t=2.26, p=0.027. And that’s the exact figures that are listed as the main effect.
We found a significant difference between conditions in performance on the dots task, t(79) = 2.26, p = .027
Result!
Let’s check it with another piece of information we have.
Participants in the green-store condition stole $0.48 more from the envelope than those in the conventional-store condition (M = $0.56, SD = $0.13, vs. M = $0.08, SD = $0.14), t(79) = 2.55, p = .013, prep = .942.
Again, unadjusted this gives us t = 15.9213, which we can safely assume is not the case. What we really want, again, is:
M = $0.56, SD = $0.13*38^0.5, vs. M = $0.08, SD = $0.14*43^0.5), t(79) = 2.55, p = .013
which is
M = $0.56, SD = $0.80, vs. M = $0.08, SD = $0.92), t(79) = 2.55, p = .013
Without playing with the rounding, this returns t=2.4898, p=0.0149; which is close enough - it will definitely jiggle close enough by playing with the decimal tails.
It seems clear at this point we’re dealing with a SD/SE error. Whoopsie.
Now, let’s complicate things. Previously, the control sample was tested against the expected baseline value of 40%, specifically:
Participants who had purchased in the conventional store identified 42.5% (SD = 2.9%) of trials as having more dots on the right side; this percentage was not significantly different from the actual percentage (i.e., 40%), t(37) = 1.66, p = .106
OK. If we run that test as described, we get t=5.3, p=homeopathy. I mean, of course it is - the mean is a whole SD from the value of interest.
But, if we use our new adjusted value that the overall effect says is right, we get t=0.8619, p=0.39.
Neither of those values are t=1.66, p=.106 as in the paper. So that’s fun.
Let’s keep going.
The next problem is: remember from the above, that this task is REALLY easy. Here’s a sample panel I knocked together in a couple of seconds.
You think you can spot which side has more dots in this presentation time?
Yep, me too. And this is 7 vs 10 - harder than the sample task parameters mentioned in the paper. If the participants are trying and completely honest, there should be a floor effect pretty close to the number of right-hand-side presentations, which is 40%. Spamming the right key to make drinking money is a ceiling of 100%.
And this is *totally* incompatible with 42.5% (17.88) or 51.4% (17.51).
To get a SPRITE panel even close to normal, we need to presume that a fair chunk of the participants (a) can’t do this task and (b) if they’re guessing, persistently guess the 0.5c rather than the 5c option. Allowing people to get as few as 20 right hand side answers is required to produce a distribution without a massive left stack.
Not great.
Summary
Experiment 1: cell sizes are confusing, and I can’t recreate them as described.
Experiment 3: confuses SD with SEM, hiding behind that there’s a 1-sampled t-test that makes no sense at all, and an overall result with some very strange means.
So now what?
In conclusion, let me clear this up: I don’t think this study is falsified, fabricated, or even necessarily problematic beyond the standards of the era. We have no evidence for that one way or the other.
I do think:
(a) taken in its entirety, I have strong concerns about the accuracy of this paper, and it should be checked by the authors and/or the journal immediately. I’ll pre-suppose that the data from an experiment conducted ~15 years ago isn’t available, because (1) it probably isn’t, and also (2) that’s what authors who prefer to avoid scrutiny inevitably say, and that is most of them. This is because at a minimum scrutiny is time consuming and annoying, and at maximum, evidence of wrongdoing. The data is so often not available, even if the paper was published last week.
Given that, in an ideal world, the journal would take some form of responsibility for making sure that *I* am not full of shit.
(b) that some combination of the original reviewers and maybe one of the 1262 citations of this paper - which I can’t check in their entirety - really should have realised even a little bit of this a long time ago. Or, if one of them did, it really should have made a difference to the trajectory of how a paper like this is considered citable in the long term. At times like this, I realise just how much the difference between looking at a paper, and REALLY looking at a paper is. I’m rusty at this, I don’t have good code resources right now, and this was … not so bad. The work was moderate, but the techniques were really quite straightforward. If you want to get Angry On The Internet about something today, I would request that it is not how the authors are terrible people out to rob the world (you don’t know ‘em and neither do I), and is about the risible amount of scrutiny that published research truly undergoes.
We are still talking about computational reproducibility (last paper I saw two days ago from time of writing) and not doing it. That article is from the old editor in chief of Psychological Science, by the way. What a mess.
(c) I am quite well aware that Dr. Mazar is an author on the now-infamous ‘signing at the top’ study that features questionable datasets from both Gino and Ariely. Like I said at the start, that’s how I found this - browsing the co-author’s work. Given that involvement, here’s what you can assume about what’s written here: nothing. Absolutely nothing. If you don’t think that bad data management, rank incompetence, mild oversights with outsized consequences, or regular garden-variety screwups can occur at EVERY point in research, and every mistake is a deliberate misdeed, then you’re just being vindictive. These twisted and limp reporting standards don’t help.
(d) it’s rarely a waste of time to revisit old cultural objects to see how much things have changed, or, how much they haven’t.



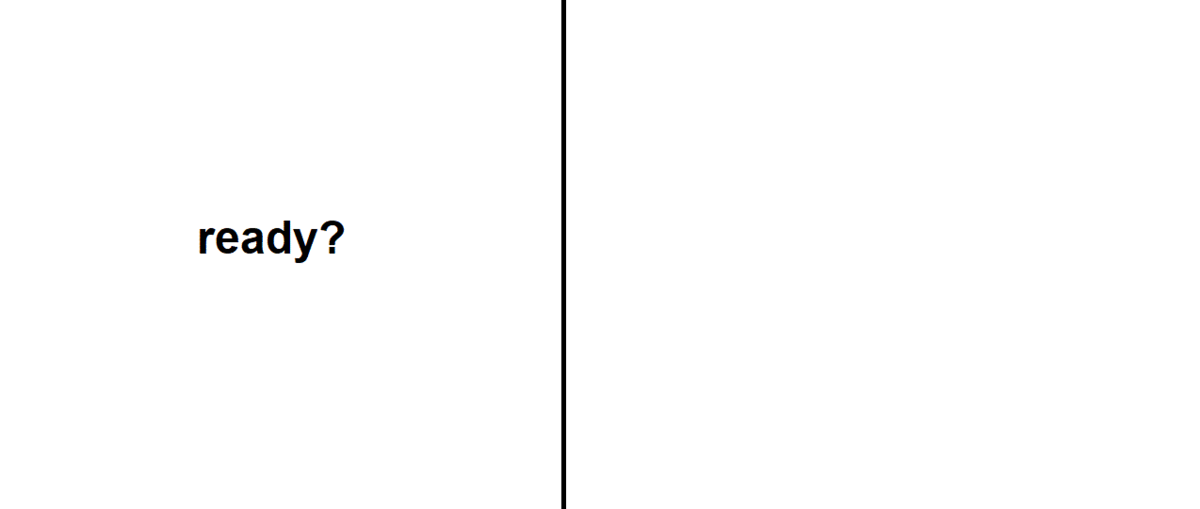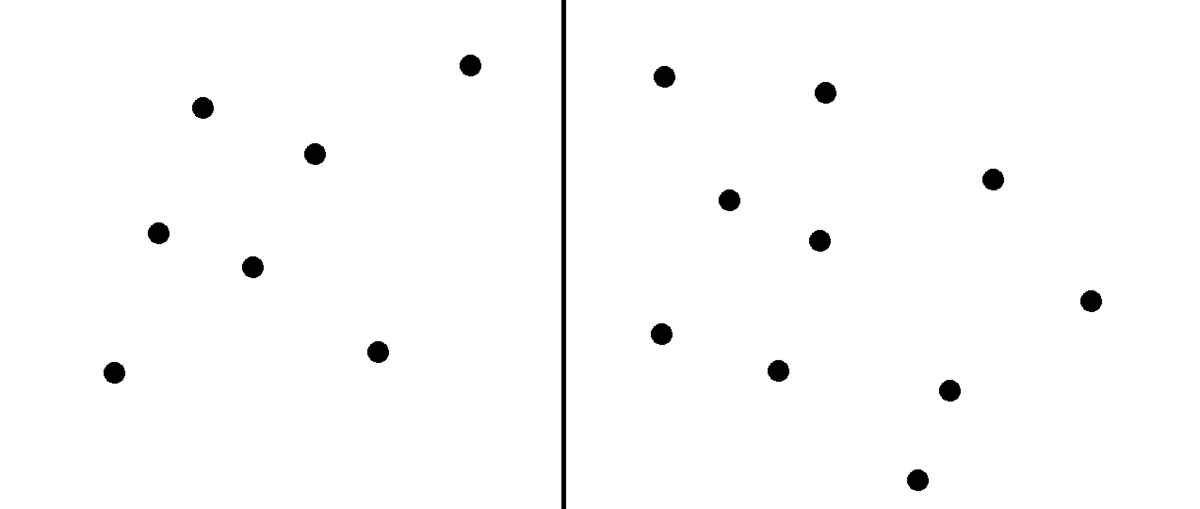
Here are some links:
https://osf.io/ryusz/
https://web.archive.org/web/20150915154355/http://www-2.rotman.utoronto.ca/facbios/file/PS_2010_MazarZhong-withCorrectionsComments.pdf
Nina Mazar posted some additional info on her OSF page about this paper.
From the comments on the pdf she uploaded:
"In this and the following paragraph, we mistakenly qualified pooled ANOVA SEs as SDs and the other way around. The corrections are noted below."
That might account for some or all of the discrepancies you found?
And from a separate summary file you can also see there:
"In December 2012 we notified Psychological Science about some errors in the reporting of the results, and requested guidance on how to submit a corrigendum. In response to our email, the editorial office informed us that our corrections were not serious enough to warrant publishing a correction. We therefore made publicly available for download an annotated version of the published paper, with our corrections in the text and in comments. This pdf used to be available since 2013 on Nina Mazar's website, while at the University of Toronto. That same file is now available on OSF."
I checked the wayback machine and that claim seems valid.